 В предыдущей статье мы рассчитывали время прилива и его высоту в яхтинге для STANDARD PORTS. Но прелесть яхтинга в том , что это не только переходы между крупными портами с известной информацией по приливам. А и путешествия по различным интересным местам, не прописанным в альманахах. Что в этом случае делать? Ничего сложного. Сейчас разберем задачу для SECONDARY PORT. В предыдущем примере мы определяли возможное время входа в марину St Malo. На самом деле планирование перехода часто начинают именно с конечной точки путешествия.
В предыдущей статье мы рассчитывали время прилива и его высоту в яхтинге для STANDARD PORTS. Но прелесть яхтинга в том , что это не только переходы между крупными портами с известной информацией по приливам. А и путешествия по различным интересным местам, не прописанным в альманахах. Что в этом случае делать? Ничего сложного. Сейчас разберем задачу для SECONDARY PORT. В предыдущем примере мы определяли возможное время входа в марину St Malo. На самом деле планирование перехода часто начинают именно с конечной точки путешествия.
Расчет времени прилива для SECONDARY PORT.
Давайте представим себе, что мы хотим стартовать из небольшого городка Binic, расположенного примерно в 40 милях пути к западу от St Malo. Сделаем еще два предположения: пусть наша скорость составляет 5 узлов, и для простоты пренебрежем течением. Таким образом, время в пути должно составить 8 часов. Всё было бы просто, но при низкой воде городок оказывается в паре миль от моря, и высота осушаемой территории достигает 6 метров. А воду в марине, чтобы лодки оставались на плаву, сдерживают ворота. Из альманаха узнаем, что ворота открываются, когда прилив превышает отметку 8.5 метра. С нашей осадкой в 2 метра это вполне достаточно для прохода. Остается определить время, когда ворота будут открыты 18 сентября. Как вы уже, наверное, догадались, городок Binic является вторичным портом для St Malo.
 Итак, нам нужно определить, в какое время высота прилива будет больше 8.5 метра. Разница во времени, как мы видим из рисунка, составляет 10 минут для показателей высокой воды, а нас интересует именно высокая вода. То есть прилив приходит в Binic на 10 минут раньше, чем в St Malo. Табличное время высокой воды: 0819-0010=0809. Прибавляем 1 час для корректировки летнего времени и получаем 0909. Это и есть время HW в Binic.
Итак, нам нужно определить, в какое время высота прилива будет больше 8.5 метра. Разница во времени, как мы видим из рисунка, составляет 10 минут для показателей высокой воды, а нас интересует именно высокая вода. То есть прилив приходит в Binic на 10 минут раньше, чем в St Malo. Табличное время высокой воды: 0819-0010=0809. Прибавляем 1 час для корректировки летнего времени и получаем 0909. Это и есть время HW в Binic.
Также просто мы можем оценить высоту прилива в Binic. Интересующая нас дата — 18 сентября — приходится на сизигию. Из альманаха (рис. 21) мы имеем значение разницы для HW, равное -0.8 метра. Таким образом, HW для Binic составляет 12.8 — 0.8=12.0 метра. Для построений нам нужно определить еще и значение LW в Binic. Таблица альманаха предлагает нам значение разницы LW, равное 0.2 метра. Следовательно, LW составляет 1.0 — 0.2=0.8 метра.
Используя кривые приливов для St Malo, производим построения. На поле для построений отмечаем рассчитанные величины LW и HW и соединяем их прямой АВ.
Вторую вертикальную прямую проводим через требуемое значение высоты прилива (НТ) — 8.5 метра. Из точки пересечения С проводим горизонтальную прямую до пересечения с кривыми приливов. Получаем точки пересечения D и Е и опускаем перпендикуляры на шкалу времени.
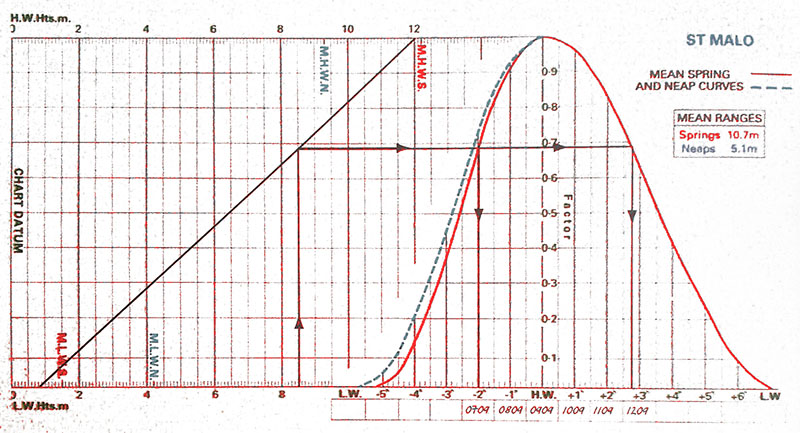
Теперь заполняем шкалу времени, зная, что табличное значение HW равно 0909. По заполненной шкале считываем значения времени, когда прилив 18 сентября составит больше чем 8.5 метра: с 7 утра до полудня. Это и есть интервал времени, когда будут открыты ворота и мы сможем покинуть марину!
Как вы помните, наша цель — St Malo. Войти в марину мы можем после 1718. Ходу нам TTG (TimeTo Go) 8 часов. Всё складывается очень удачно. Предлагаем выйти из Binic в 9 утра, и если погода будет благоприятна, нас ждут хорошая марина и вкусный ужин в красивом городе.
На практике часто встречаются ситуации, когда отличия времени и высоты прилива в стандартных и вторичных портах существенны. Более того, для некоторых интервалов времени они известны заранее, а для других — их приходится вычислять, решая задачу интерполяции.
Следует учесть, что очень часто задача определения высоты прилива требует не точного расчета, а оценки. Ведь если время выхода из марины — это вопрос дисциплины на судне, то точно рассчитать время прихода для малого судна, особенно парусного, практически невозможно. Конечно, перед выходом мы узнаем прогноз погоды и делаем план перехода, но это только прогноз. Достаточно небольшого изменения ветра или волнения, и расчеты приходится переделывать.
Метод двенадцатых расчета время прилива.
Ранее мы определили, что приливы — это очень длинные волны. И их форму в открытом море можно достаточно точно апроксимировать синусоидой. В прибрежный зонах приливы, взаимодействуя с береговой линией, меняют внешние очертания, и приливные кривые могут иметь форму, представленную на рисунке ниже. Обратите внимание на различие формы кривых для сизигии и квадратуры.
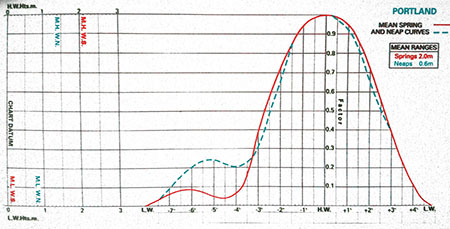 Однако для большинства мест, а также если нам недоступна приливная кривая, можно пользоваться методом, основанным на характеристиках синусоиды, который получил название «Метод двенадцатых».
Однако для большинства мест, а также если нам недоступна приливная кривая, можно пользоваться методом, основанным на характеристиках синусоиды, который получил название «Метод двенадцатых».
Если мы принимаем, что изменение уровня воды описывается синусоидой, то для определения значения уровня воды в любой момент времени нам необходимо знать время и значения ближайших HW и LW. Разность HW и LW даст нам амплитуду прилива (Tidal Range).
Математически точно: высота прилива за первый час уменьшается на 1/12 от Tidal Range, за второй час — на 2/12, за третий и четвертый часы-на 3/12, за пятый-на 2/12 и за шестой — на 1/12. Итого за 6 часов изменений высоты прилива равно Tidal Range.
Это простой метод, дающий достаточно точную оценку и не требующий сложных построений.
Для примера давайте этим методом решим задачу определения возможного времени преодоления порога в St Malo. Как мы помним из условий задачи, необходимая высота прилива составила:
Required Height of Tide = Draft + Safety Clearance + Sill = 2 +1 + 2 = 5 метров.
А из таблиц мы получили: в 15 часов 19 минут LW 1.0 метра, в 20 часов 35 минут HW 12.9 метра. Обратите внимание, что время от низкой до высокой воды не всегда равно 6 часам. Поэтому, пользуясь Методом двенадцатых, нужно привязываться или к HW, или к LW. Давайте в нашем примере привяжемся к HW.
Важно не забыть произвести корректировку летнего времени. Прибавляя один час, мы получим, что высокая вода 18 сентября в St Malo во второй половине дня наступит в 2135.
Попробуем произвести необходимые построения в таблице на рисунке ниже.
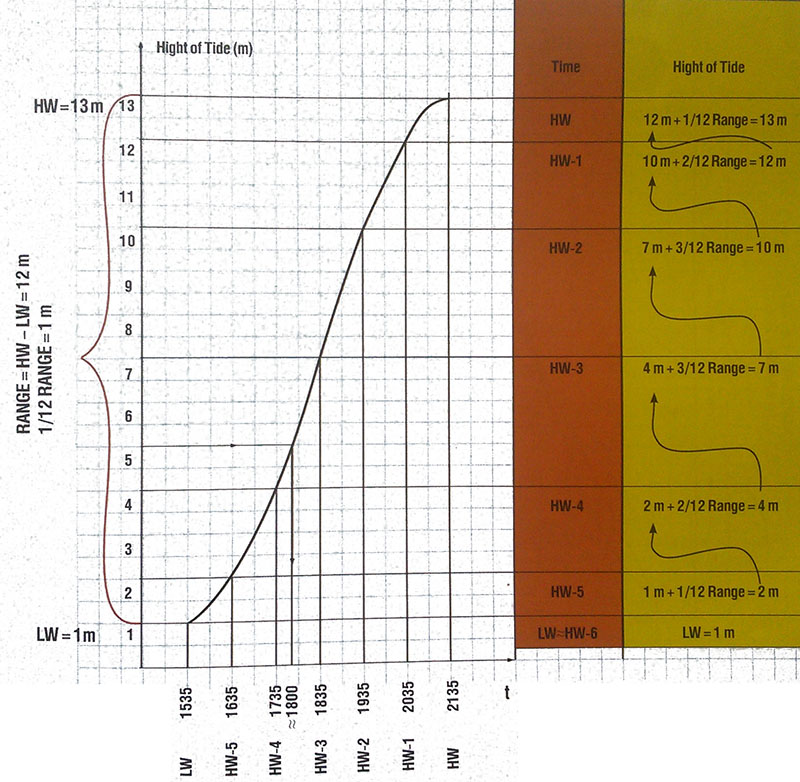
Мы видим, что высота прилива в 1735 будет 4 метра, а в 1835 -уже 7 метров. Очевидно, что 5 метров высоты прилива будет где-то посередине. Оценив это время как 1800, мы получим ошибку всего в 30 минут от точного решения по приливной кривой. Согласитесь, неплохой результат.
Запомните, что быстрее всего изменяется высота прилива посередине между моментами, когда вода достигает значений HW и LW. Следовательно, в это время и скорость приливного течения, как правило, будет максимальной.
Правило четвертей и десятых расчета время прилива.
Еще один эффективный метод, основанный на законах геометрии, позволяющий быстро получать оценку высоты прилива, называется 0NE-QUARTER/0NE-TENTH RULE. Это правило иллюстрируется на рисунке .
Для примера возьмем те же исходные данные, которыми мы пользовались при изучении Метода двенадцатых.
Нам потребуется листок бумаги в клетку, и на нем мы проведем следующие построения:
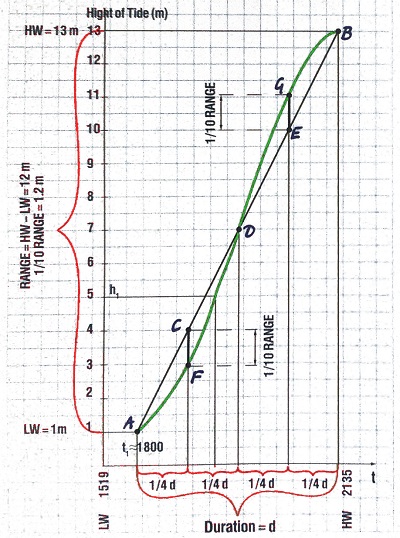 1. На оси абсцисс отложим отрезок времени между LW и HW.
1. На оси абсцисс отложим отрезок времени между LW и HW.
2. На оси ординат отложим отрезок, соответствующий значениям LW и HW.
3. Построим прямую АВ, соединяющую точки для LW и HW.
4. Разделим отрезок времени между LW и HW на 4 равных части и восстановим перпендикуляры до пересечения с прямой АВ, получив тем самым точки С, D и L
5. От точки С отложим вниз отрезок, равный 1/10 разности между LW и HW, получив тем самым точку F. А от точки Е -такой же отрезок вверх, получив точку G.
6. Теперь на глаз плавной кривой соединим точки A, F, D, G и В. Полученная кривая является математически корректной аппроксимацией синусоиды, а как мы уже отмечали выше, для большинства случаев именно она описывает кривую приливов.
7. По данному графику легко для любого времени t1, получить текущее значение высоты прилива h1
Неудивительно, что результаты, полученные двумя методами, совпали: оба метода основаны на одном и том же предположении, что приливная кривая имеет форму синуса. Чем вам пользоваться, зависит от того, что вам сейчас удобнее — поупражняться в арифметике или провести графические построения.
На этом расчеты определения высоты прилива в конкретном месте и в конкретное время закончим, а в следующей статье перейдем к расчетам приливного течения.